[lbbrudsk] deriving the quaternion multiplication table

the diagram below describes how to derive the off-diagonal entries of the quaternion multiplication table from ijk = -1 .  apply the multiplication operation indicated by the label on each arrow to both sides of the equation, then use ii = jj = kk = -1 to annihilate factors.  quaternion multiplication is associative (by definition), and multiplication by -1 is commutative.  an exhaustive proof of consistency therefore has 16 parts, one for each arrow direction, which William Rowan Hamilton presumably worked out all in his head while walking by the bridge -- pretty impressive.

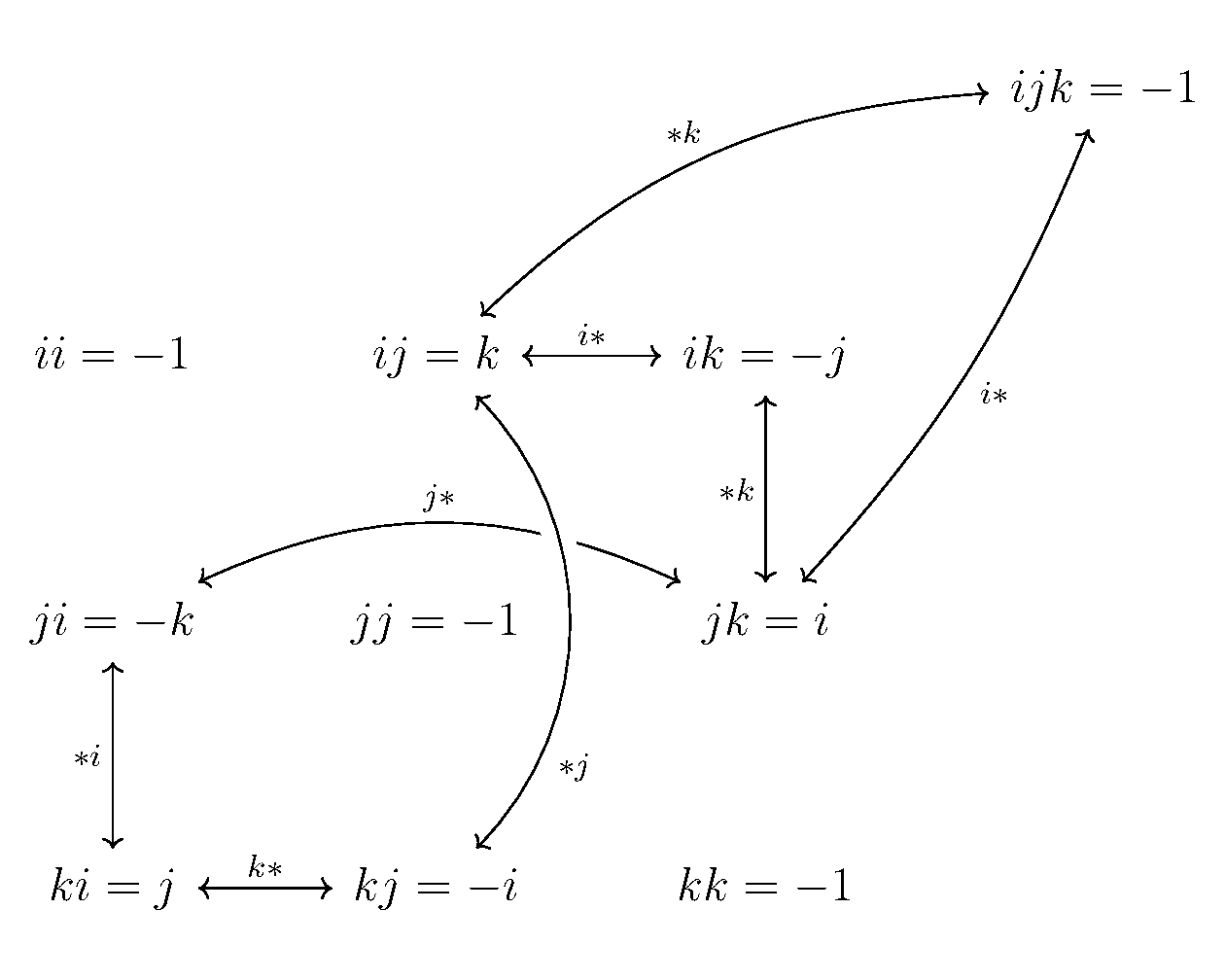
every arrow is double-ended: applying the same operation twice always brings you back to where you started.  this is a consequence of i^2 = j^2 = k^2 = -1.  applying the same operation twice equates to multiplication by -1, and then we cancel out the minus sign.

LaTEX source, using ticzcd (commutative diagrams):

\usepackage{tikz-cd}

\newcommand{\mytimes}{*} % or \cdot

\begin{document}

% the direction of the arrow affects which side of the arrow the label goes
\begin{tikzcd}[row sep=9ex]
& & & ijk = -1 \ar[ldd,bend left=10,"i\mytimes",leftrightarrow]\\
ii=-1 & ij = k \ar[r,"i\mytimes",leftrightarrow] \ar[rru,bend left=20,"\mytimes k",leftrightarrow] & ik = -j & \\
ji = -k \ar[rr,bend left=25,"j\mytimes" ,leftrightarrow] & jj = -1 & jk = i \ar[u,"\mytimes k",leftrightarrow] & \\
ki = j \ar[r,"k\mytimes",leftrightarrow] \ar[u,"\mytimes i",leftrightarrow] & kj = -i \ar[from=uu,bend left=45,"\mytimes j" near end,leftrightarrow, crossing over] & kk=-1 &
\end{tikzcd}

previously, multiplication table of the icosahedral group.