asymptotic elliptic integral

I discover that y=ellip(1-t)-1; behaves like 0.25*(-t.*log(t)+t*v) in the neighborhood of t=0, for v=1.77259; where ellip(x)= complete elliptic integral of the second kind. (Later,) v= 4*log(2)-1 from expanding the function around t=1. With one pole out of the way, the function should be a little more amenable to Chebyshev approximation; however, there are still an infinite number of poles at t=1 at higher order.

Ramanujan and Ellipses

Most of Ramanujan's work is not practically useful. However, two exceptions are his formulae for the approximate circumference (perimeter) of an ellipse. Here is the simpler one:

P ~= pi [ 3(a+b) - sqrt((3a+b)(a+3b)) ]

It can be calculated on a standard basic calculator with one register of memory that doesn't obey algebraic operator precedence (times before plus, etc.)

3*a+b=P3*b+a=*RK=QSPa+b=*3=PR*3.141592654=

where P= "M+", R= "MR", K="MC", Q="sqrt", S="+/-". It is a little annoying that a and b need to be typed in 3 times each.

This formula can also be expressed in terms of h=[(a-b)/(a+b)]², although it's not so helpful for the simple calculator.

P = pi (a+b) [ 3 - sqrt( 4-h ) ]

This formula has 12th order error in eccentricity and worst case relative error of 3.8% (about two decimal digits of precision)

Ramanujan's second formula is more accurate:
P ~= pi (a+b) [ 1 + 3h / ( 10+ sqrt( 4-3h )) ] or on a simple calculator: a+b=Pa-b=/RK*=P*3=S+4=Q+10/3/RK=P1/RK=Pa+b=*R*3.141592654=

This formula has 20th order error in eccentricity and worst case relative error of 0.40% (about 3 decimal digits of precision). David W. Cantrell has added a correction term to Ramanujan's ellipse perimeter formula

                       3h                            12
  pi(a + b) (1 + ----------------- + (4/pi - 14/11) h  ).
                 10 + Sqrt(4 - 3h)

which decreases the worst case error to 0.0014% (about 5 decimal digits of precision). However it no longer seems possible to calculate this formula with only one register of memory.

(What expressions can be calculated with one register of memory?)

Ramanujan came up with his formulae in 1914; Cantrell's correction term is only May 2004. It's interesting that while the circumference of a circle has been laid to rest for thousands of years, improvements in the circumference of an ellipse still continue to this day.

Some matlab code for the Gauss-Kummer series

for i=1:200,n=sym(i),coeff2(i)=(prod((n+1):2*n)/prod(1:n)/((1-2*n)*(-4)^n))^2;end xac2=vpa((1+sum(h.^(1:200).*coeff2))*pi*(a+b),1000)

Cayley series
cay=sym(1)+x/4*(log(16/x)-1);for i=2:100,n=sym(i),cay=cay + x^n * prod(1:2:(2*n-3))^2 * (2*n-1) / (prod(2:2:(2*n-2))^2*(2*n))/2 * (log(16/x)+sum(-4./((1:2:2*n-1) .* (2:2:2*n)))+2/(2*n-1)/(2*n));end

exact value via elliptic integral
[m1,m2]=ellipke(double(1-b*b/a/a)); 4*double(a)*m2

h=(a-b)/(a+b);h=h*h
p3=vpa(pi*(a+b)*(1+3*h/(10+sqrt(4-3*h))),120)
sc=4/sym(pi)-sym(14)/sym(11)
p4=vpa(pi*(a+b)*(1+3*h/(10+sqrt(4-3*h)) + sc*h^12),120)

For Halley's comet, with e=0.9673 and a=17.94AU= 2,683,786,326 km (forget significant digits, and all rounding is by truncation), its perimeter (via 200 terms of Gauss Kummer) is 11,529,383,201.15 km. Ramanujan's first formula underapproximates by 1,175,193.9 km. Second underapproximates by 2637.7 km, and Cantell's correction formula only does slightly better, being under by 2616.4 km.

For a=4, b=3, (a 3-4-5 right triangle), which has 0.66 eccentricity, its perimeter is 22.1034921607095050452855864638724607782782891. Ramanujan's second formula (with or without correction) misses by -1.8e-12 For a=12, b=5 (another right triangle), e=0.9091, perimeter=55.6959493710847386662875219855831134524807, and Ramanujan's second formula (with our without correction) misses by -2.3e-7.

For a=1 b=1/10, e=0.9949 perimeter=4.063974180100895742557793101181576, second formula -4.6e-5, with correction -3.2e-5. For a=1 b=1/100 e=0.99995, perimeter = 4.00109832972265186074746449610774074592667795549222896254442786221, no correction -9.5e-4, with correction -0.49e-4. For a=1 b=1/1000 e=0.9999995, perimeter = 4.00001558810468824461075647365734692443, no correction -15.1e-4, with correction 0.21e-4.

Things for which exact formulae exist: circle perimeter, circle area, ellipse area, ellipsoid area for ellipsoid that have circular cross sections, ellipsoid volume

No exact formulae: ellipse perimeter, general ellipsoid surface area.

Below is a picture of the approximation error of various formulae. Blue is Ramanujan's second formula, green includes Cantrell's correction term, red is Cantrell's 2001 formula involving Hoelder means, cyan is Cantrell's 2004 formula.

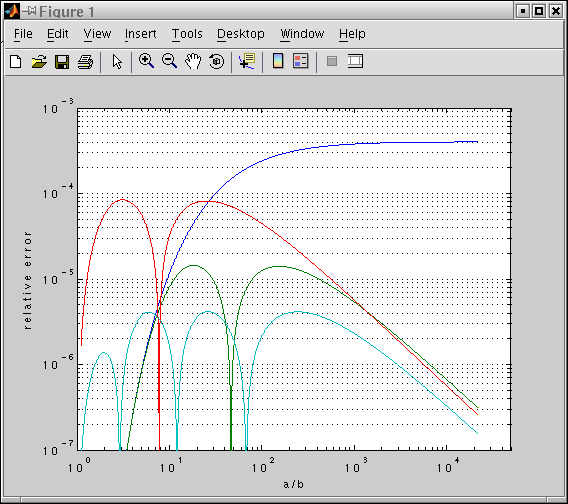
>> sc=4/pi-14/11;a=1;p=0.825;k=74;p2=0.410117;
>> i=0.1:0.001:10;
>> t=exp(i);b=1./t;xc=ellip(1-b.*b)*4;h=((a-b)./(a+b)).^2;v=pi*(a+b);n=1+3*h./(10+sqrt(4-3*h)); p3=v.*n;p4=v.*(n+sc*h.^12);h2=4*(a+b)-2*(4-pi)*((a+b.^-p)/2).^(1/-p);
>> h3=4*(a+b)-2*(4-pi)*a*b./(p2*(a+b)+(1-2*p2)/(k+1).*sqrt((a+k*b).*(k*a+b)));
>> loglog(t,((xc-p3)./xc),t,(abs(xc-p4)./xc),t,(abs(h2-xc)./xc),t,(abs(h3-xc)./xc))

Ambidextrously

Ambidextrously (14 letters) might be the longest word in the English language that does not contain any letter more than once.

Isogram

Square roots of negative identity

sqrt(-I) for I=1 is not defined in the reals. However, for I=eye(2), there are solutions. For example [0 1 ; -1 0]² = [-1 0 ; 0 -1]. The general solution in reals (thanks to Matlab) seems to be [-d, b ; -(1+d²)/b, d]. For 3x3 matrices there appear to be no solutions, so it seems like an odd-even dimensions thing.

Generalizations of complex numbers

Quaternions follow the rule ``i²=j²=k²=ijk=-1'' (which must suck for people who don't know the ordering of the English alphabet). From this we can derive ij=k, jk=i, ki=j, and reversal negates: ji=-k kj=-i ik=-j. from which we can get the squaring rule (a+bi+cj+dk)² = (a²-b²-c²-d²)+2abi+2acj+2adk Squaring is interesting because z:=z²+c yields fractals. Next idea: complex numbers of complex numbers, where we recursively apply the "square the second component to get the negative of the first component" rule. The normal way to write it out would be with coordinates, but I'll try ijk notation and see what happens: ((a,b),(c,d))²= (a+bi+cj+dk)²= (a²-b²-c²+d²)+(2ab-2cd)i+(2ac-2bd)j+(2bc+2ad)k The multiplication table looks like

    1  i  j  k
  * ----------
1 | 1  i  j  k
i | i -1  k -j
j | j  k -1 -i
k | k -j -i -1

Generalizing complex numbers to 3-vectors of the form (a,(b,c)) runs into the problem of how to define the result of X+(Y,Z) to be a scalar.

Voice interfaces

Speech-recognition interfaces for computers would be good for choosing between many items. I specifically would like to see it for switching betwen applications (MacOS X already sort of does this) and switching between different windows (or buffers, or tabs) within an application. One would need a way to record the name of "this buffer". Perhaps there is something special in its good for changing or choosing among things which don't have a "constant" name. Because if it had a constant name, you could define a shortcut (or bookmark, or hot key, etc.) for it.

Antipodes

On the opposite side of the earth from me is the Indian Ocean, which isn't interesting. Where are the points on land which whose antipode is also on land? What does that set of points look like when plotted on a globe? One can also ask what are the land/water points and the water/water points, though they aren't so interesting.

Automatically Figuring Out Acronyms

There ought to be a web service, probably powered by a search engine, that figures out acronyms. For example, if someone wanted to know what, say, MIT stands for, one would look for webpages containing the keywords MIT "M* I* T*", the latter being a wildcarded keyword of three consecutive words starting with the letters M, I, and T. Of course it's harder than that because of small filler words like "of", and other weird ways acronyms and abbreviations are formed.

Slashdot | LOAF - Distributed Social Networking Over Email

Slashdot | LOAF - Distributed Social Networking Over Email Bloom Filters are neat (and I've used a similar them for DNA motif discovery). One could create a bloom filtered image of all substrings of length N in your hard drive, and then send it to a antivirus or anti-adware company for analysis.

Factoring Benchmarks

Some fun things to do if you have Pari/GP installed. echo "print(factorint(fibonacci(990)))" | /usr/bin/time gp for(i=1, 100000, print("The factors of (10^50)+", i, " are"); print(factor(10^50+i)," time=", gettime()/60000.0, " minutes")) Feel free to replace 10^50 with 10^60 or 10^70.

Common Document Structure Paradigm

Many websites (or documents in general) have the following general structure: (1) Table of Contents (2) Main text referring to: (3) Figures. Instead of being completely general about how content of a page, HTML (or whatever its successor might be) and future browsers ought to be designed to ``do this common case well.'' The simplest version might be: navigation bar across the top; scrollable left column of text with hyperlinks to figures; scrollable right column of figures, which automatically scroll to the right place when a left-column hyperlink is clicked. A few fancy features: Each figure has a "Hide" check box so that an arbitary subset of figures can be compared. Left/Right columns can be swapped to Top/Bottom orientation.

Baseball teams sorted in order

Baseball teams sorted in order by date of mathematical elimination from the playoffs. I wonder if any team has been eliminated yet.

The handheld toy that everyone

The handheld toy that everyone wants: A GPS flashlight cell-phone radio gameboy PDA camera MP3 player remote-control.

Bit compression by a byte compressor

I wonder how well various compression programs, e.g., gzip, bzip2, do on strings that are repetitive at the bit level, but not so obviously repetitive when the bits are packed into bytes. For example consider repeating a 33-bit pattern 32*N times (for a total of of 132*N bytes). A good compressor should asymptotically get a compression factor of 32*N, while a bad one might only get a factor of N (or 8*N?). It's also an interesting problem to prevent repeative occurrence of bytes for this problem. One wants to select a bitstring such that windows of size 8 are all unique.

Least Primitive Root of Mersenne Primes

Least Primitive Root of Mersenne Primes: All the more reason the C217 composite cofactor of 2^1101+1 ought to be factored. The final terms of the sequence were calculated using the Mersenne factorizations mentioned earlier. The earlier terms were calculated using znprimroot in Pari/GP. Proving a primitive root X of a prime p requires modular exponentiation of X to all powers (p-1)/q where q is a prime factor of (p-1). At first I thought it had to be to all divisors of (p-1), which would have required something like 2^50 work for 2^2281-1; fortunately, it was not.

The least primitive root of M2203 is at least 3, and it probably is 3. 3 is probably the least primitive root for M4253, M9689, M21701, as well. This comes from the observation that 2 never seems to be a primitive root. When 3 is not a primitive root, then 3^((p-1)/3)==1 (mod p) empirically. It's interesting that all mersenne primes except the first seem to have remainder 1 when divided by 3 (true for all odd exponents).

for(i=2, length(p), if((Mod(3,2^p[i]-1)^((2^p[i]-2)/3))!=Mod(1,2^p[i]-1), print(p[i]))) where p is a list of mersenne exponents.

P-1 for some of the higher Mersenne prime exponents are surprisingly smooth: 216090 = 2*3*3*5*7*7*7*7, 20996010 = 2*3*3*3*3*5*7*7*23*23. These would be more interesting targets for the ElevenSmooth project than their number 2*2*2*2*2*2*3*3*3*5*5*7*11 = 3326400

In an unrelated topic, in June I submitted a superseeker query for [7,11,32,40,75,87,136,152,215,235,312,336,427], but I no longer know the significance of the sequence. I think it might have something to do with the Pell Equation. The generating function guesser generated the continuation [455, 560, 592, 711, 747, 880], which I recall the first few terms being correct.

Capillary Effect

It's interesting how capillary action can make water flow uphill. I wonder if this effect can be harnessed to create an analogue computer for solving tricky optimization problems. Simulated annealing works because uphill steps are allowed, to escape local minima.

A four player card game

Inspired by the paper by Euler, I've come up with a four-player card game. I hereby dub this game "Euler's Coincidence", in honor of the guy who analyzed it. North and East are partners on a team, and likewise South and West (so not like bridge). North gets the clubs, South the spades, East the Hearts, West the Diamonds. On each turn each player places a card on the table and they all simultaneously flip. The game is over if cards of like color match in number. If black cards match, North/East wins 1 point. If red cards match, South/West wins 1 point. On a match, everybody gets their 13 cards back and the game begins anew. Otherwise, the four cards are discarded and play continues. (Note that if (for example) a black 6 and a red 6 appear, then it's not a match.) So therefore, North and West are seeking a match with the player across from them, and South and East are trying to avoid matching. Of course, the optimal play is to play your cards in random order. The game might need to be tweaked still to make people avoid that. Stay tuned for future tweaks.

Negative First Cousin

Cousins (first cousins) share a common grandparent. Second cousins share a common great-grandparent. Third cousins a common great-great-grandparent. Extrapolating the other direction: Zeroth cousins share a common parent and are usually called siblings. Negative first cousins share a common identity: I am my (only) negative first cousin.

Keywords with periods around them

Dear Google, I searched for the keyword 54286614780461303 and got no results. However, the page http://www.mersenneforum.org/showthread.php?t=1544 does contain the keyword. This page is in your archive (I found it by other keywords). The problem seems to be because the keyword is embedded within a string "blah.54286614780461303.blah". My suggestion is that you treat periods as word separators. (You can still also continue to index the longer string with periods embedded.)

A pen with a downward

A pen with a downward pointing light built in to it for writing in the dark.