Ramanujan and Ellipses

Most of Ramanujan's work is not practically useful. However, two exceptions are his formulae for the approximate circumference (perimeter) of an ellipse. Here is the simpler one:

P ~= pi [ 3(a+b) - sqrt((3a+b)(a+3b)) ]

It can be calculated on a standard basic calculator with one register of memory that doesn't obey algebraic operator precedence (times before plus, etc.)

3*a+b=P3*b+a=*RK=QSPa+b=*3=PR*3.141592654=

where P= "M+", R= "MR", K="MC", Q="sqrt", S="+/-". It is a little annoying that a and b need to be typed in 3 times each.

This formula can also be expressed in terms of h=[(a-b)/(a+b)]², although it's not so helpful for the simple calculator.

P = pi (a+b) [ 3 - sqrt( 4-h ) ]

This formula has 12th order error in eccentricity and worst case relative error of 3.8% (about two decimal digits of precision)

Ramanujan's second formula is more accurate:
P ~= pi (a+b) [ 1 + 3h / ( 10+ sqrt( 4-3h )) ] or on a simple calculator: a+b=Pa-b=/RK*=P*3=S+4=Q+10/3/RK=P1/RK=Pa+b=*R*3.141592654=

This formula has 20th order error in eccentricity and worst case relative error of 0.40% (about 3 decimal digits of precision). David W. Cantrell has added a correction term to Ramanujan's ellipse perimeter formula

                       3h                            12
  pi(a + b) (1 + ----------------- + (4/pi - 14/11) h  ).
                 10 + Sqrt(4 - 3h)

which decreases the worst case error to 0.0014% (about 5 decimal digits of precision). However it no longer seems possible to calculate this formula with only one register of memory.

(What expressions can be calculated with one register of memory?)

Ramanujan came up with his formulae in 1914; Cantrell's correction term is only May 2004. It's interesting that while the circumference of a circle has been laid to rest for thousands of years, improvements in the circumference of an ellipse still continue to this day.

Some matlab code for the Gauss-Kummer series

for i=1:200,n=sym(i),coeff2(i)=(prod((n+1):2*n)/prod(1:n)/((1-2*n)*(-4)^n))^2;end xac2=vpa((1+sum(h.^(1:200).*coeff2))*pi*(a+b),1000)

Cayley series
cay=sym(1)+x/4*(log(16/x)-1);for i=2:100,n=sym(i),cay=cay + x^n * prod(1:2:(2*n-3))^2 * (2*n-1) / (prod(2:2:(2*n-2))^2*(2*n))/2 * (log(16/x)+sum(-4./((1:2:2*n-1) .* (2:2:2*n)))+2/(2*n-1)/(2*n));end

exact value via elliptic integral
[m1,m2]=ellipke(double(1-b*b/a/a)); 4*double(a)*m2

h=(a-b)/(a+b);h=h*h
p3=vpa(pi*(a+b)*(1+3*h/(10+sqrt(4-3*h))),120)
sc=4/sym(pi)-sym(14)/sym(11)
p4=vpa(pi*(a+b)*(1+3*h/(10+sqrt(4-3*h)) + sc*h^12),120)

For Halley's comet, with e=0.9673 and a=17.94AU= 2,683,786,326 km (forget significant digits, and all rounding is by truncation), its perimeter (via 200 terms of Gauss Kummer) is 11,529,383,201.15 km. Ramanujan's first formula underapproximates by 1,175,193.9 km. Second underapproximates by 2637.7 km, and Cantell's correction formula only does slightly better, being under by 2616.4 km.

For a=4, b=3, (a 3-4-5 right triangle), which has 0.66 eccentricity, its perimeter is 22.1034921607095050452855864638724607782782891. Ramanujan's second formula (with or without correction) misses by -1.8e-12 For a=12, b=5 (another right triangle), e=0.9091, perimeter=55.6959493710847386662875219855831134524807, and Ramanujan's second formula (with our without correction) misses by -2.3e-7.

For a=1 b=1/10, e=0.9949 perimeter=4.063974180100895742557793101181576, second formula -4.6e-5, with correction -3.2e-5. For a=1 b=1/100 e=0.99995, perimeter = 4.00109832972265186074746449610774074592667795549222896254442786221, no correction -9.5e-4, with correction -0.49e-4. For a=1 b=1/1000 e=0.9999995, perimeter = 4.00001558810468824461075647365734692443, no correction -15.1e-4, with correction 0.21e-4.

Things for which exact formulae exist: circle perimeter, circle area, ellipse area, ellipsoid area for ellipsoid that have circular cross sections, ellipsoid volume

No exact formulae: ellipse perimeter, general ellipsoid surface area.

Below is a picture of the approximation error of various formulae. Blue is Ramanujan's second formula, green includes Cantrell's correction term, red is Cantrell's 2001 formula involving Hoelder means, cyan is Cantrell's 2004 formula.

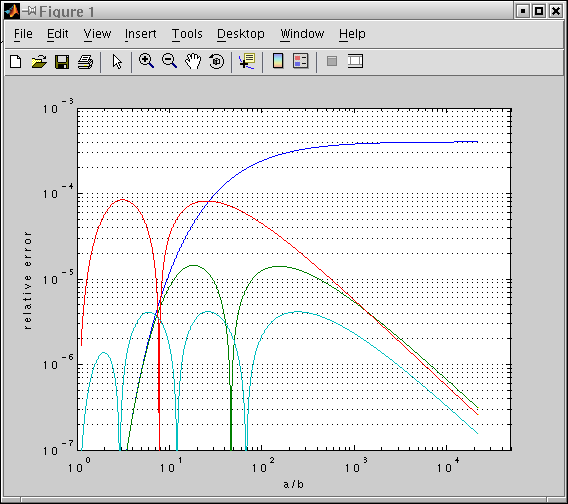
>> sc=4/pi-14/11;a=1;p=0.825;k=74;p2=0.410117;
>> i=0.1:0.001:10;
>> t=exp(i);b=1./t;xc=ellip(1-b.*b)*4;h=((a-b)./(a+b)).^2;v=pi*(a+b);n=1+3*h./(10+sqrt(4-3*h)); p3=v.*n;p4=v.*(n+sc*h.^12);h2=4*(a+b)-2*(4-pi)*((a+b.^-p)/2).^(1/-p);
>> h3=4*(a+b)-2*(4-pi)*a*b./(p2*(a+b)+(1-2*p2)/(k+1).*sqrt((a+k*b).*(k*a+b)));
>> loglog(t,((xc-p3)./xc),t,(abs(xc-p4)./xc),t,(abs(h2-xc)./xc),t,(abs(h3-xc)./xc))