[dvxljvju] Cornu spiral

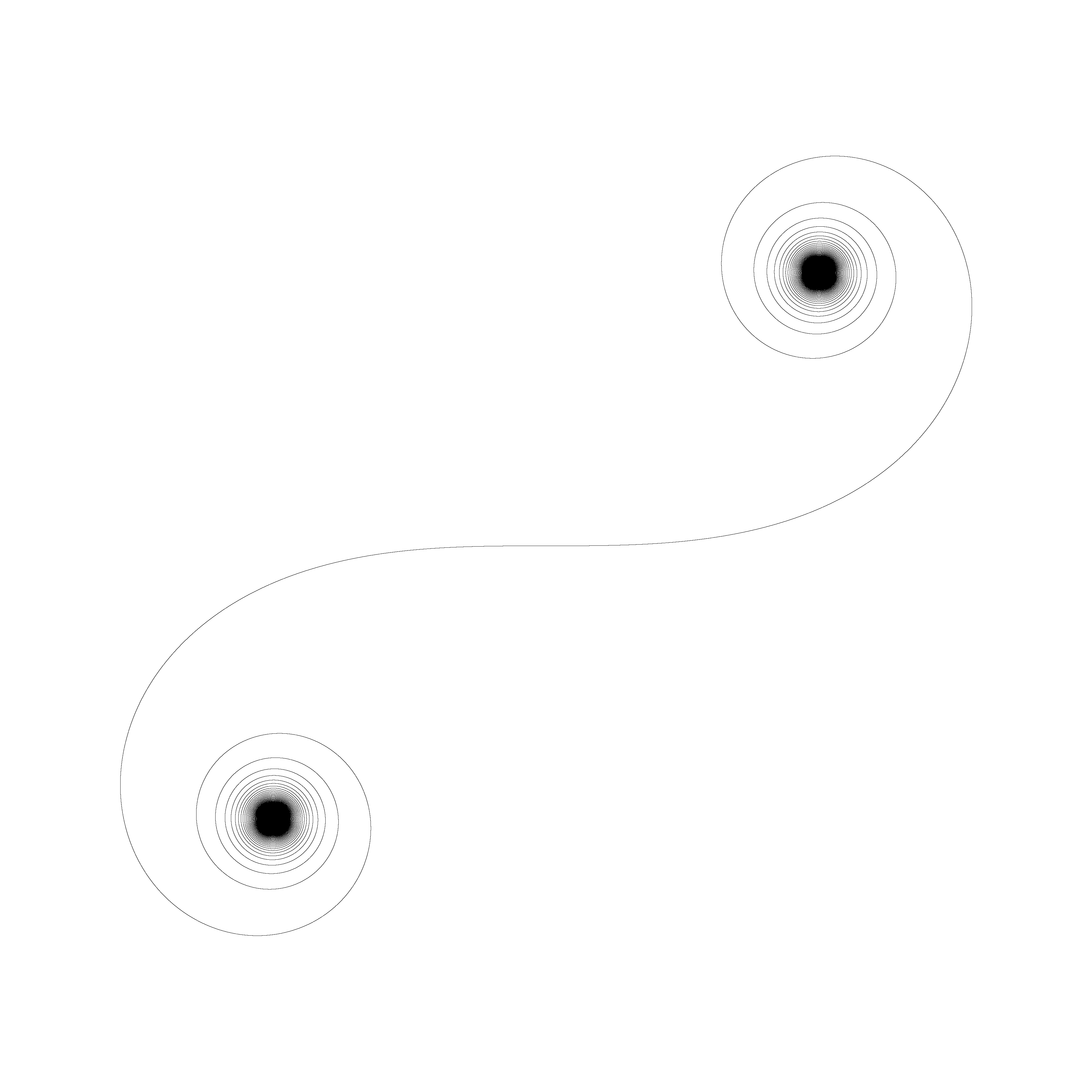
Most of the images of the Cornu spiral (a.k.a. clothoid, Euler spiral) that I could find "give up" in plotting the spiral long before it approaches the limit point (the center of the spiral), giving the incorrect impression that the spiral converges to a circle and not a point.

Below are some images of the Cornu spiral that follow the spiral far enough that all the pixels near the center are black.  Going to t=1500 was sufficient.  We used this Cephes implementation of the Normalized Fresnel integral function, with bugs fixed by SciPy.  Here is the source code of the Cornu spiral plotter, along with the images available for download at full resolution.

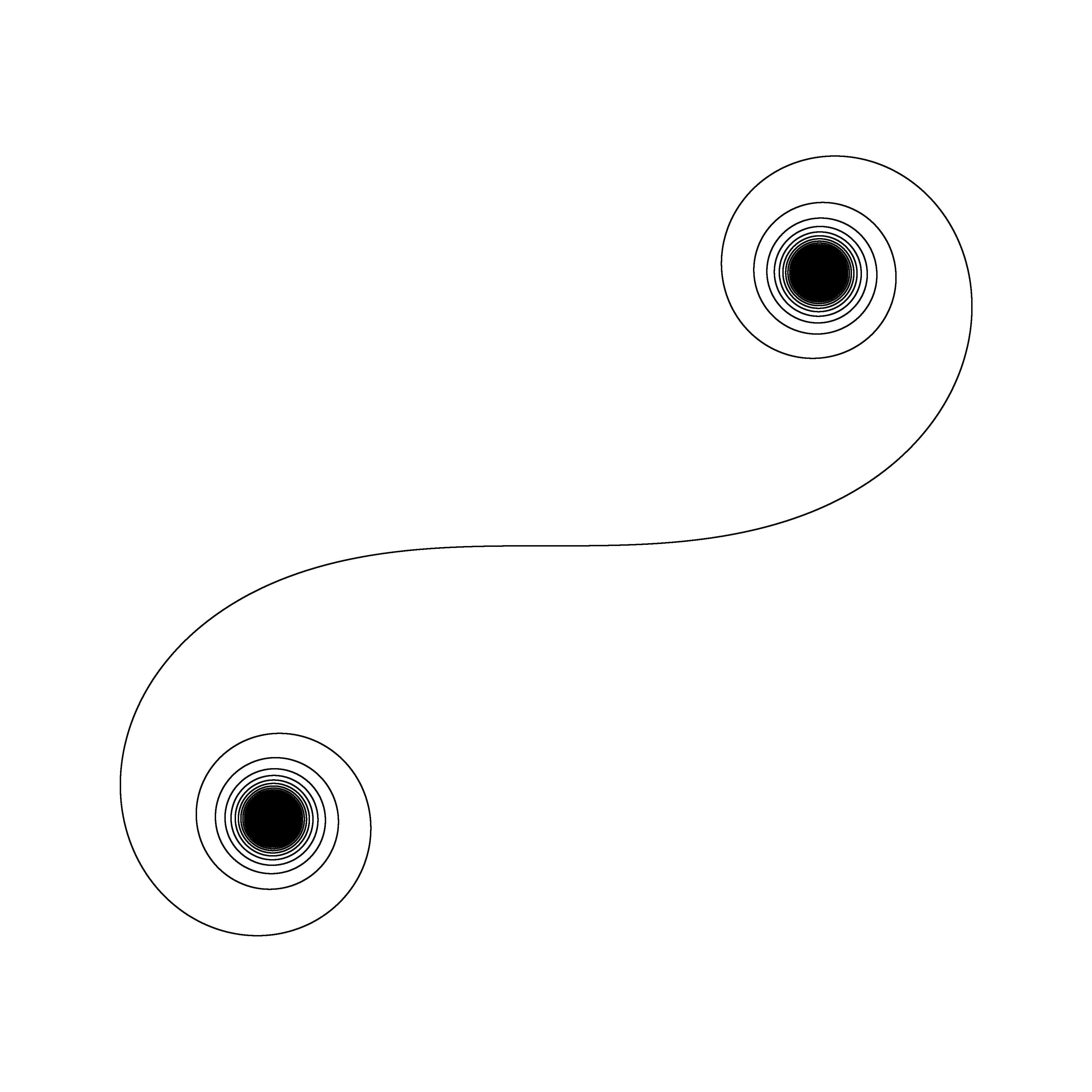
This one was plotted with a thicker line width:

Future projects:

The spiral looks like the integral symbol, mirrored and rotated.  Create some art substituting the spiral for the integral symbol in the definition of the Fresnel integrals: S(t) = integral from 0 to t of sin(x^2) dx, etc.  This should be easy.

Plotting the spiral as a path requires choosing how wide to make the pen as well as complexities (e.g., antialiasing) regarding how to plot points that don't fall exactly on a pixel.  Avoid some of these complexities as follows.  Divide the plane in half with the diagonal line y=x.  This creates a bunch of regions bounded by the spiral and the diagonal line.  Color the regions like a checkerboard, avoiding coloring adjacent regions the same color.

Or, dynamically adjust the pen width to keep it appropriate for where we are in the spiral.

Is the Cornu spiral with the normalized Fresnel integrals different, other than in scale, from the one using unnormalized Fresnel integrals?