[jozupeos] Small factors of central binomial coefficients

We investigate how many times some small primes {2,3,5,7} divide central binomial coefficients c(n)=binomial(2*n,n).

For example, c(6) = 12 choose 6 = 924 = 2^2 * 3^1 * 5^0 * 7^1 * (higher factors), so the exponents are 2,1,0,1.  We write zero as period in the table below to distinguish zeroes from nonzeros.

	2^x	3^x	5^x	7^x
0 choose 0	.	.	.	.
2 choose 1	1	.	.	.
4 choose 2	1	1	.	.
6 choose 3	2	.	1	.
8 choose 4	1	.	1	1
10 choose 5	2	2	.	1
12 choose 6	2	1	.	1
14 choose 7	3	1	.	.
16 choose 8	1	2	1	.
18 choose 9	2	.	1	.
20 choose 10	2	.	.	.
22 choose 11	3	1	.	1
24 choose 12	2	.	.	1
26 choose 13	3	.	2	1
28 choose 14	3	3	2	.
30 choose 15	4	2	1	.
32 choose 16	1	2	1	.
34 choose 17	2	3	1	.
36 choose 18	2	1	2	1
38 choose 19	3	1	2	1
40 choose 20	2	2	1	1
42 choose 21	3	1	1	.
44 choose 22	3	1	1	.
46 choose 23	4	3	2	.
48 choose 24	2	2	2	.
50 choose 25	3	2	.	2
52 choose 26	3	3	.	2
54 choose 27	4	.	.	2
56 choose 28	3	.	1	1
58 choose 29	4	1	1	1
60 choose 30	4	.	.	1
62 choose 31	5	.	.	1
64 choose 32	1	2	.	2

It seems p does not divide c(p^n) for p>2.  For p=2, 2 divides c(2^n) exactly once, probably from the 2 in the definition of c(n).

Here are some bar graphs revealing a fractal structure.  The horizontal axis goes from n=0 to 1199, that is, from (0 choose 0) to (2398 choose 1199); the vertical axis is stretched by a factor of 50.

2^x

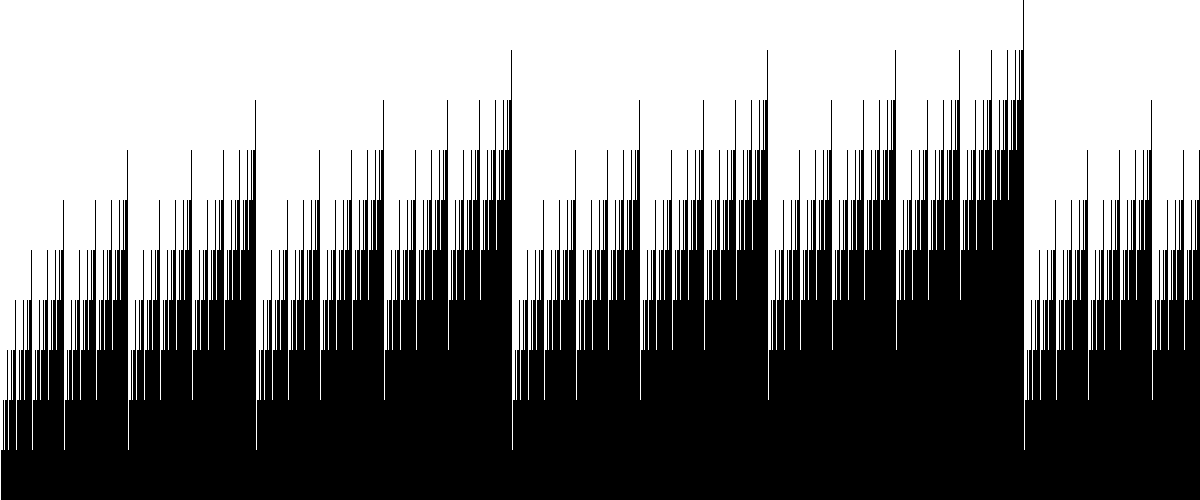
3^x

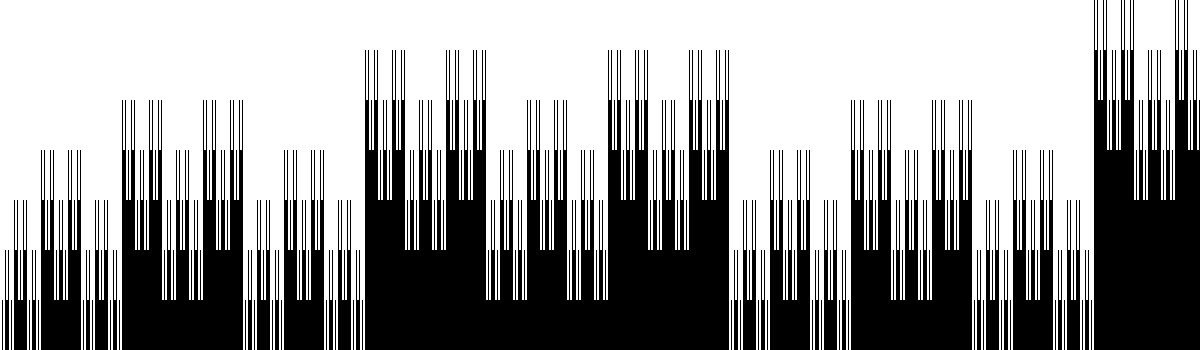
5^x

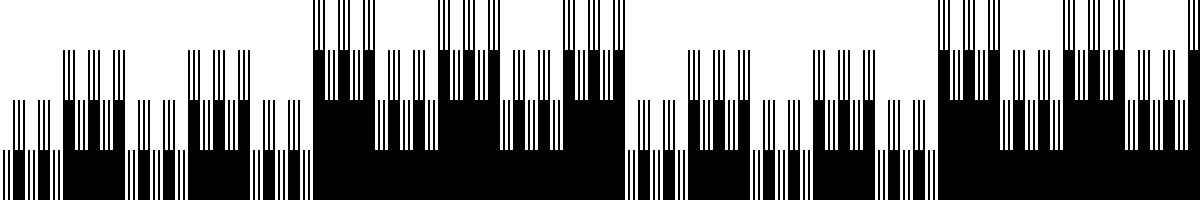
7^x

Haskell source code.